Aspectos físicos de la visión humana
Leonardo Dimieri
Director: Gustavo Gasaneo
La Física
Descripción de objetos y sus interacciones
¿Seres vivos...?
Descripción del ojo
- Anatomía del ojo
- Fisiología ocular
- Músculos
Óptica ocular
- Formación de imágenes
Sistema nervioso
- Retención de imágenes
- Percepción visual
Movimientos oculares
- Movimientos de persecución
- Sacadas y micro-sacadas
Modelo físico
- Modelado de músculos
- Dinámica ocular
Conclusiones
- Perspectivas
Anatomía del ojo humano
La órbita
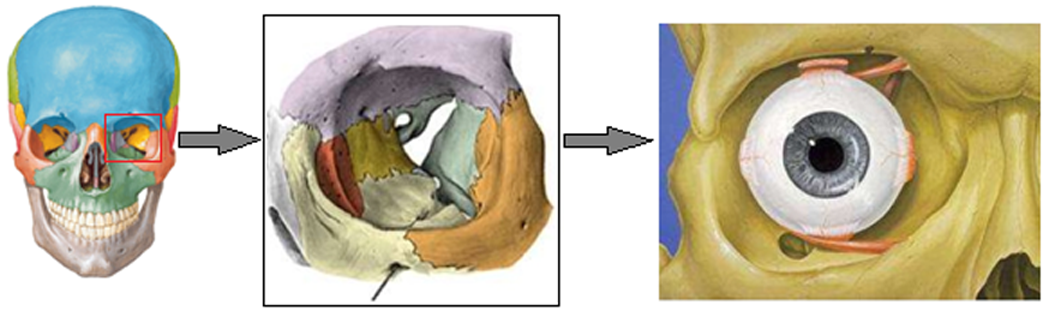
Fisiología del ojo
Córnea
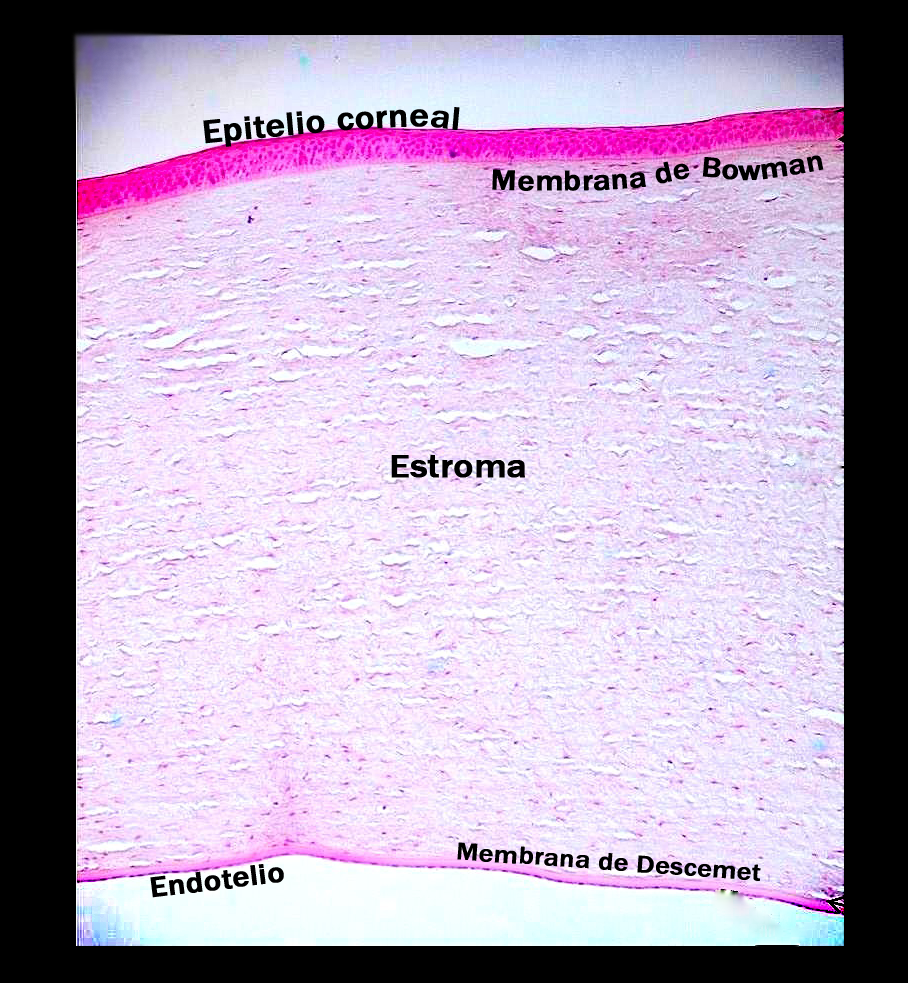
Componentes de la
Túnica vascular
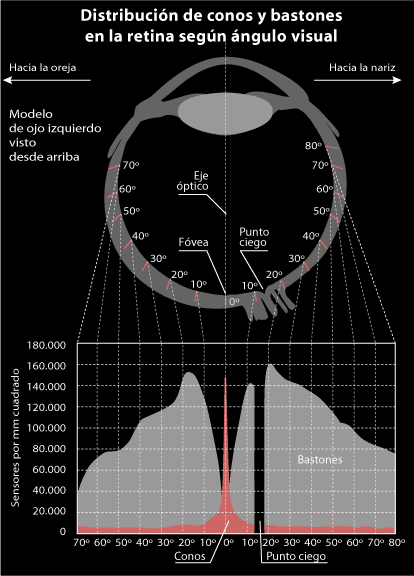
La retina
Músculos del ojo
Óptica ocular
Formación de imágenes


Sistema Nervioso
Percepción
¿Cómo vemos?
Cubo de Necker
Movimientos oculares
Modelo físico
Modelado de los músculos
Modelo de Hill (1938)
Componente muscular activa
$F_{act}=F_0 f_l(\tilde{l}_m)f_v(\tilde{v}_m) a(t)$Curvas de $f_l(\tilde{l}_m)$ y $f_v(\tilde{v}_m)$
Activación muscular
Difusión de Calcio en los músculos
$\frac{da(t)}{dt}+[ \frac{1}{\tau_{act}}(\beta+(1-\beta)u(t))] a(t)=\frac{1}{\tau_{act}}u(t)$donde
$ 0 < \beta <1 $ y $\tau_{act}$es una constante de activación temporal que varia de acuerdo con cuán rápido o cuán lento sea el músculo.
Fuerza elástica del tendón
$\dot{F}_t=K_t(F_t)\dot{l}_t$donde $K_t(F_t)$ representa la relación entre la fuerza y la longitud del tendon y está dada por $k_{tc}F_t+k_{tl}$ si $0 \leq F_t < F_{tc}$ o por $k_s$ si $F_t \geq F_{tc}$
Fuerza total que ejerce el músculo
$F_m=F_{pe}+F_{act}+B_m \dot{l}_m$Zajac y Wicke (1984); He et al (1991)
Como el músculo es isovolumétrico, $l_w$ debe permanecer constante y se cumple:
$\dot{\alpha}=-\frac{\dot{l}_m}{l_m}\tan \alpha $La ecuación para el músculo de masa Mm es
$M_m \frac{d^2(l_m \cos \alpha)}{dt^2}=F_t - (F_{act}+F_{pe}+B_m \dot{l}_m)\cos \alpha$o bien
$M_m \ddot{l}_m = F_t \cos \alpha - \cos^2 \alpha (F_{act}+F_{pe} +B_m \dot{l}_m) + \frac{M_m \dot{l}_m^2 \tan^2 \alpha}{l_m}$Dinámica ocular
Considerando los 6 músculos, la ecuación de momentos es
$(\vec{r}_{ri}\times \vec{F}_{ri})+(\vec{r}_{re}\times \vec{F}_{re})+$$+(\vec{r}_{os}\times \vec{F}_{os})+(\vec{r}_{oi}\times \vec{F}_{oi}) +(\vec{r}_{om}\times \vec{F}_{om})+(\vec{r}_{om}\times \vec{F}_{om})+ \vec{M}_{s}= J_G \dot{\vec{\omega}}$
donde $\vec{r}_{ij}$ representa el brazo de palanca de cada uno de los músculos y $F_{ij}$ representan las fuerzas de los músculos correspondientes. $\vec{M}_{s}$ representa al momento pasivo generado por el septum, es decir, la resistencia al movimiento impuesta por la viscocidad de la órbita en la que se soporta el ojo
Movimientos sacádicos horizontales
Involucra solamente 2 músculos
Representación fisica del ojo
Las ecuaciones de movimiento quedan
$J_G \ddot{\Theta}+B_G \dot{\Theta}+K_G \Theta=F_{t1}-F_{t2}$donde $J_G$ es el momento de inercia del globo ocular, $B_G$ la viscozidad y $K_G$ su elasticidad
Las ecuaciones para el músculo-tendón
$\frac{M}{980}\ddot{l}_{mi}+B_{pm}(\frac{180}{\pi r}) \dot{l}_{m1}=F_{ti}-F_{acti}-F_{pe1}(l_{mi})$
para los músculos recto interno y recto externo (i=1,2). Asumiendo una forma exponencial para la fuerza pasiva del músculo:

Además:
$\dot{F}_{t}=K_t(F_t) (\frac{180}{\pi r}) \dot{l}_{t}$
Las ecuaciones de la dinámica músculo-tendón quedan:
$\dot{F}_{t1}=K_t(F_{t1})[-\dot{\Theta}-(\frac{180}{\pi r}) \dot{l}_{m1}]$para el músculo interno, y
$\dot{F}_{t2}=K_t(F_{t2})[\dot{\Theta}-(\frac{180}{\pi r}) \dot{l}_{m2}]$
para el músculo externo
Utilizando la notación del vector de estado:
$x^T(t)=[\Theta \, \, \, \dot{\Theta} \, \, \, l_{m1} \, \, \, \dot{l}_{m1} \, \, \, l_{m2} \, \, \, \dot{l}_{m2} \, \, \, F_{t1} \, \, \, F_{t2} \, \, \, a_1 \, \, \, a_2]$Las ecuaciones de movimiento quedan:
Simulaciones
Utilizando el vector de estado inicial:
$x^T(0)=[0 \, \, \, 0 \, \, \, 4 \, \, \, 0 \, \, \, 4 \, \, \, 0 \, \, \, 20 \, \, \, 20 \, \, \, .17 \, \, \, .17]$(Tomados del trabajo de Robinson, 1964, así como también los datos de los parámetros involucrados)
Se resolvió numéricamente el sistema en Mathematica
Resultados
Movimiento sacádico de 10° (Posición-tiempo)

Resultados
Movimiento sacádico de 10° (Velocidad-tiempo)

Variaciones en parámetros
Momento de inercia Jg y Viscosidad Bg
Conclusiones
- Constitución fisiológica del ojo
- Óptica de la visión
- Músculos
- Percepción
- Movimientos oculares
- Compensación de adaptación neuronal
- Modelo físico de los músculos
- Modelo para la dinámica ocular
- Se pretende estudiar el modelo en función de la variación de los parámetros
- Se desea extraer información de los tiempos involucrados en poner en marcha el sistema oculomotor para tener una idea más clara de los tiempos de análisis cerebrales